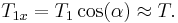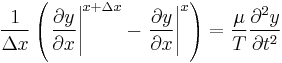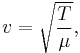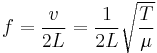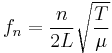Vibrating string
A vibration in a string is a wave. Usually a vibrating string produces a sound whose frequency in most cases is constant. Therefore, since frequency characterizes the pitch, the sound produced is a constant note. Vibrating strings are the basis of any string instrument like guitar, cello, or piano.
Contents |
Wave
The speed of propagation of a wave in a string ( ) is proportional to the square root of the tension of the string (
) is proportional to the square root of the tension of the string ( ) and inversely proportional to the square root of the linear density (
) and inversely proportional to the square root of the linear density ( ) of the string:
) of the string:
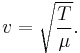
Derivation
Let 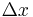 be the length of a piece of string,
be the length of a piece of string,  its mass, and
its mass, and  its linear mass. If the horizontal component of tension in the string is a constant,
its linear mass. If the horizontal component of tension in the string is a constant,  , then the tension acting on each side of the string segment is given by
, then the tension acting on each side of the string segment is given by
If both angles are small, then the tensions on either side are equal and the net horizontal force is zero. From Newton's second law for the vertical component, the mass of this piece times its acceleration,  , will be equal to the net force on the piece:
, will be equal to the net force on the piece:
Dividing this expression by  and substituting the first and second equations obtains
and substituting the first and second equations obtains
The tangents of the angles at the ends of the string piece are equal to the slopes at the ends, with an additional minus sign due to the definition of beta. Using this fact and rearranging provides
In the limit that 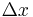 approaches zero, the left hand side is the definition of the second derivative of
approaches zero, the left hand side is the definition of the second derivative of  :
:
This is the wave equation for 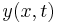 , and the coefficient of the second time derivative term is equal to
, and the coefficient of the second time derivative term is equal to 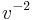 ; thus
; thus
where  is the speed of propagation of the wave in the string. (See the article on the wave equation for more about this). However, this derivation is only valid for vibrations of small amplitude; for those of large amplitude,
is the speed of propagation of the wave in the string. (See the article on the wave equation for more about this). However, this derivation is only valid for vibrations of small amplitude; for those of large amplitude, 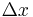 is not a good approximation for the length of the string piece, the horizontal component of tension is not necessarily constant, and the horizontal tensions are not well approximated by
is not a good approximation for the length of the string piece, the horizontal component of tension is not necessarily constant, and the horizontal tensions are not well approximated by  .
.
Frequency of the wave
Once the speed of propagation is known, the frequency of the sound produced by the string can be calculated. The speed of propagation of a wave is equal to the wavelength  divided by the period
divided by the period  , or multiplied by the frequency
, or multiplied by the frequency  :
:
If the length of the string is  , the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so
, the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so  is half of the wavelength of the fundamental harmonic. Hence:
is half of the wavelength of the fundamental harmonic. Hence:
where  is the tension,
is the tension,  is the linear density, and
is the linear density, and  is the length of the vibrating part of the string. Therefore:
is the length of the vibrating part of the string. Therefore:
- the shorter the string, the higher the frequency of the fundamental
- the higher the tension, the higher the frequency of the fundamental
- the lighter the string, the higher the frequency of the fundamental
Moreover, if we take the nth harmonic as having a wavelength given by 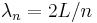 , then we easily get an expression for the frequency of the nth harmonic:
, then we easily get an expression for the frequency of the nth harmonic:
And for a string under a tension T with density  , then
, then
Observing string vibrations
One can see the waveforms on a vibrating string if the frequency is low enough and the vibrating string is held in front of a CRT screen such as one of a television or a computer (not of an oscilloscope). This effect is called the stroboscopic effect, and the rate at which the string seems to vibrate is the difference between the frequency of the string and the refresh rate of the screen. The same can happen with a fluorescent lamp, at a rate which is the difference between the frequency of the string and the frequency of the alternating current. (If the refresh rate of the screen equals the frequency of the string or an integer multiple thereof, the string will appear still but deformed.) In daylight, this effect does not occur and the string will appear to be still, but thicker and lighter, due to persistence of vision.
A similar but more controllable effect can be obtained using a stroboscope. This device allows the frequency of the xenon flash lamp to be exactly matched to the frequency of vibration of the string; in a darkened room, this clearly shows the waveform. Otherwise, one can use bending or, perhaps more easily, by adjusting the machine heads, to obtain the same frequency, or a multiple of, the AC frequency to achieve the same effect. For example, in the case of a guitar, the bass string pressed to the third fret gives a G at 97.999 Hz; with a slight adjustment, a frequency of 100 Hz can be obtained, exactly one octave above the alternating current frequency in Europe and most countries in Africa and Asia. In most countries of the Americas, where the AC frequency is 60 Hz, one can start from A# at 116.54 Hz, on the fifth string at the first fret, to obtain a frequency of 120 Hz.
See also
- String instruments
- Fretted instruments
- Musical acoustics
- Pitch (music)
- Vibrations of a circular drum
- Melde's experiment
- 3rd Bridge (harmonic resonance based on equal string divisions)
References
- Molteno, T. C. A.; N. B. Tufillaro (September 2004). "An experimental investigation into the dynamics of a string". American Journal of Physics 72 (9): 1157–1169. Bibcode 2004AmJPh..72.1157M. doi:10.1119/1.1764557.
- Tufillaro, N. B. (1989). "Nonlinear and chaotic string vibrations". American Journal of Physics 57 (5): 408. Bibcode 1989AmJPh..57..408T. doi:10.1119/1.16011.